排序

# 排序分类

第一类：比较类 1.交换排序：冒泡、快排 2.插入排序：简单插入、希尔 3.选择排序：简单选择、堆排序 4.归并排序：二路归并、多路归并
第二类：非比较 1.计数排序 2.桶排序 3.基数排序

# 复杂度

算法复杂度

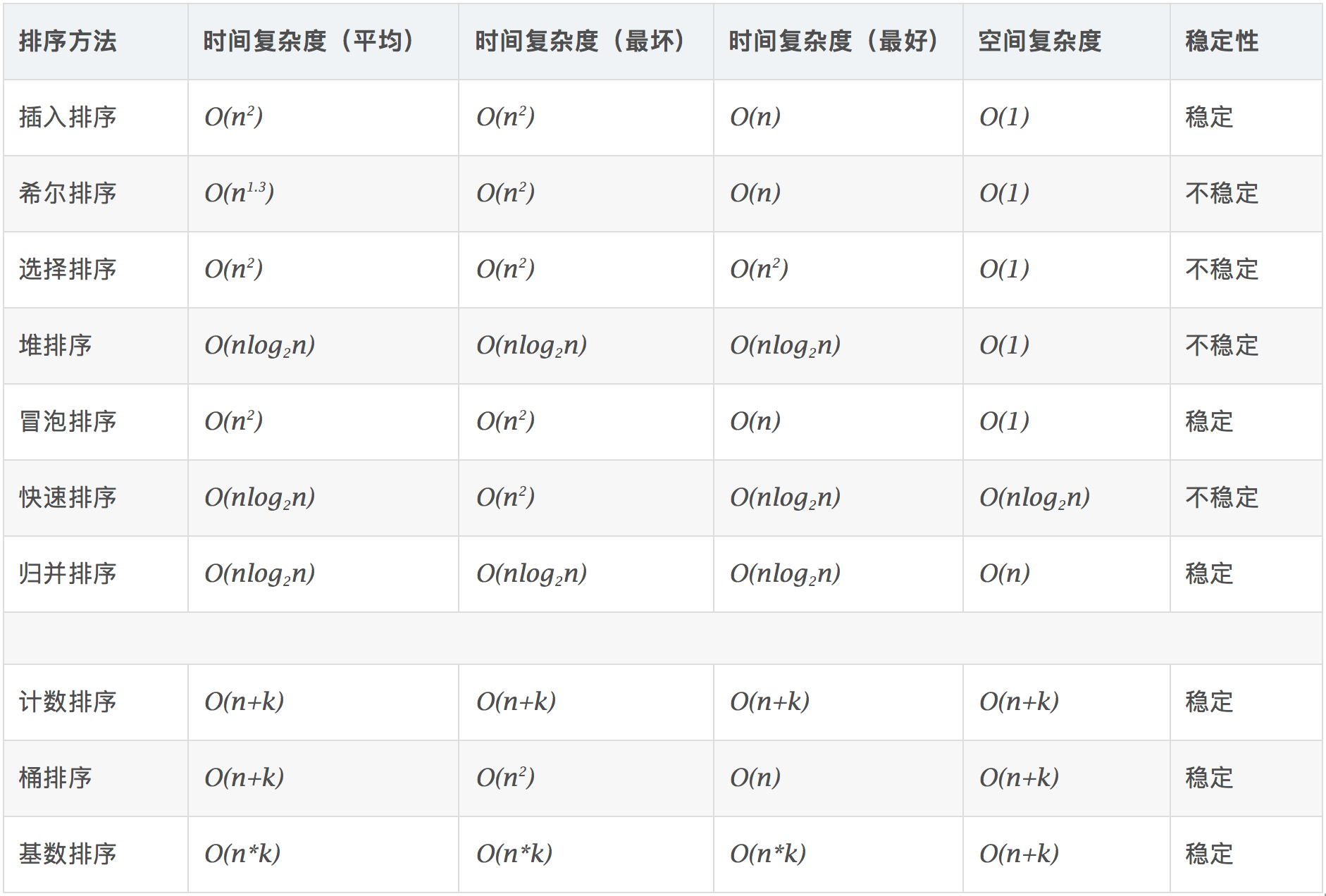
# 案例

# 冒泡排序

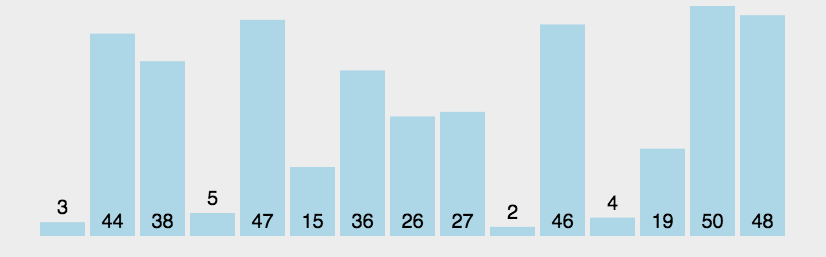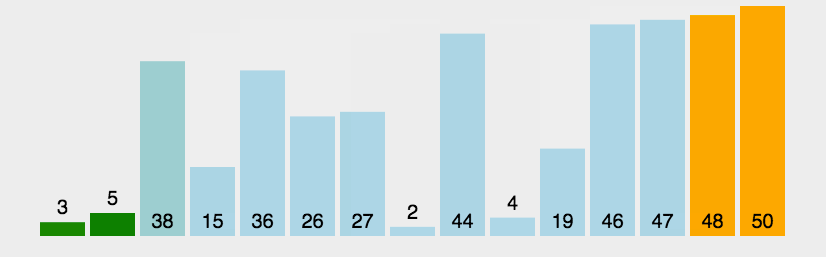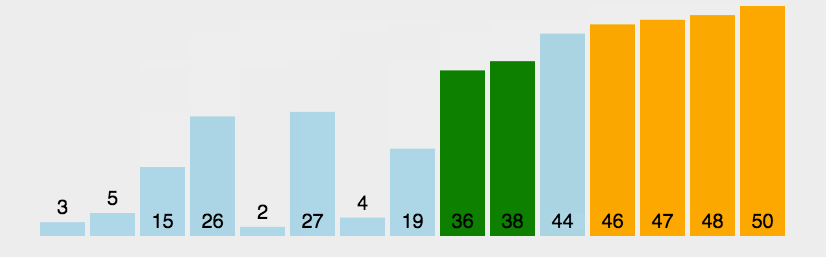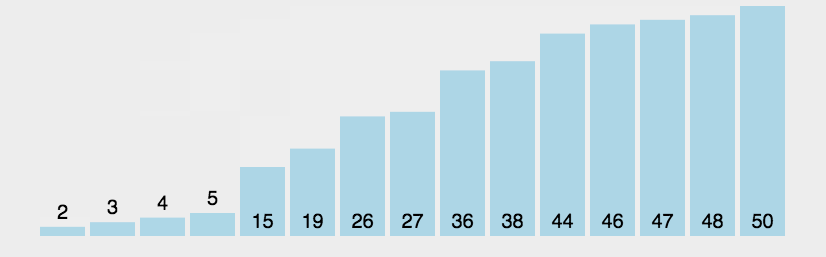
import copy

# data = [1, 3, 99, 353, 23, 55, 89, 3, 1, 5, 89, 66, -5]
data = [1, 3, 99, 353, 23, 55, 89, 3, 70, 5, 30, 66, 1000]


# 1.冒泡排序:
# 它重复地走访过要排序的数列，一次比较两个元素，如果它们的顺序错误就把它们交换过来。
# 走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。
# 这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
def mao_pao(nums: list, reverse: bool = False):
    for i in range(1, len(nums)):
        for j in range(len(nums) - i):
            if (nums[j] < nums[j + 1]) == reverse:  # 相邻元素两两比较
                nums[j], nums[j + 1] = nums[j + 1], nums[j]
    return nums


data1 = copy.deepcopy(data)
mao_pao(data1)
print('1.冒泡1：', data1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

# 选择排序

import copy


# 2.选择排序:
# 首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，
# 然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。
# 以此类推，直到所有元素均排序完毕。
def xuan_ze(nums: list):
    for i in range(len(nums) - 1):
        for j in range(i + 1, len(nums)):
            if nums[i] > nums[j]:
                nums[i], nums[j] = nums[j], nums[i]


def xuan_ze2(nums: list):
    for i in range(len(nums) - 1):
        min_index = i
        for j in range(i, len(nums)):
            if nums[min_index] > nums[j]:
                min_index = j
        if min_index == i:
            continue
        nums[i], nums[min_index] = nums[min_index], nums[i]


data2 = copy.deepcopy(data)
xuan_ze(data2)
print('2.选择1：', data2)
data2_1 = copy.deepcopy(data)
xuan_ze2(data2_1)
print('2.选择2：', data2_1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

# 插入排序

import copy

# 3.插入排序:它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。
def cha_ru(nums: list):
    for i in range(1, len(nums)):
        current = nums[i]
        tmp_index = i
        while tmp_index > 0 and nums[tmp_index - 1] > current:
            nums[tmp_index] = nums[tmp_index - 1]
            tmp_index -= 1
        nums[tmp_index] = current


data3 = copy.deepcopy(data)
cha_ru(data3)
print('3.插入1：', data3)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

# 希尔排序

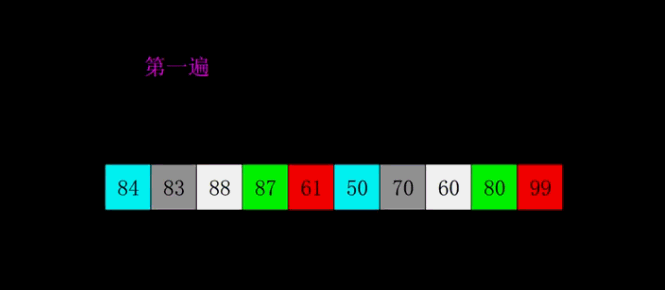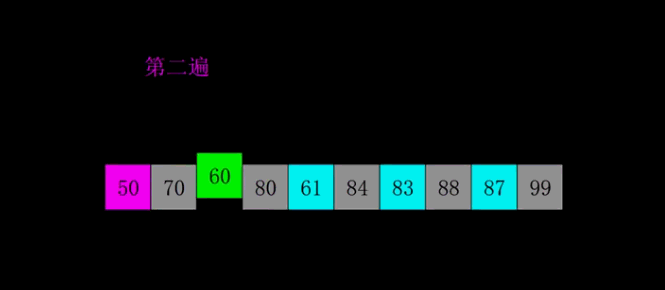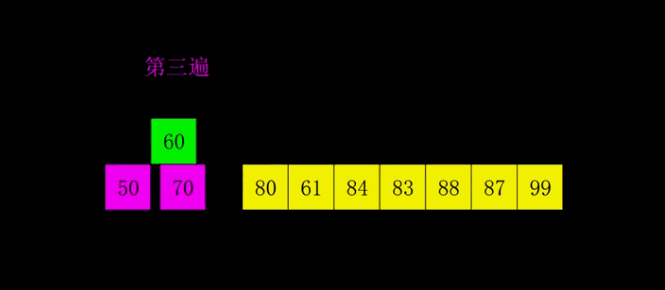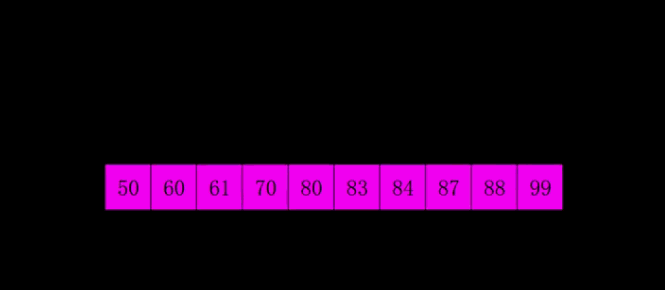
import copy


# 4.希尔排序
def xi_er(nums: list):
    gap = len(nums) // 2
    while gap > 0:
        for i in range(gap, len(nums)):
            while i >= gap and nums[i - gap] > nums[i]:
                nums[i - gap], nums[i] = nums[i], nums[i - gap]
                i -= gap
        gap //= 2


data4_1 = copy.deepcopy(data)
xi_er(data4_1)
print('4.希尔1：', data4_1)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

# 归并排序

import copy


# 5.归并排序
def gui_bing(nums: list) -> list:
    if len(nums) <= 1:
        return nums
    step = len(nums) // 2
    left = gui_bing(nums[: step])
    right = gui_bing(nums[step:])
    return gui(left, right)


def gui(left: list, right: list) -> list:
    l, r = 0, 0
    result = []
    while l < len(left) and r < len(right):
        if left[l] < right[r]:
            result.append(left[l])
            l += 1
        else:
            result.append(right[r])
            r += 1
    result += left[l:]
    result += right[r:]
    return result


data5 = copy.deepcopy(data)
print('5.归并1：', gui_bing(data5))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

# 快速排序

import copy


# 6.快速排序
def kuai_su(nums: list) -> list:
    if len(nums) <= 1:
        return nums
    mid = nums[0]  # 为了防止该值为最大或最小，可以优化，选择三个数进行比较，选择中位数
    left, right = [], []
    for num in nums[1:]:
        if num < mid:
            left.append(num)
        else:
            right.append(num)
    return kuai_su(left) + [mid] + kuai_su(right)


data6 = copy.deepcopy(data)
print('6.快速1：', kuai_su(data6))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

# 堆排序

import copy


# 7.堆排序
# 堆：一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点
def da_dui(nums: list, start: int, end: int):
    # 堆调整方法
    root = start
    child = root * 2 + 1  # 左孩子(索引)
    while child <= end:
        if child + 1 <= end and nums[child] < nums[child + 1]:
            child += 1
        if nums[root] < nums[child]:
            nums[root], nums[child] = nums[child], nums[root]
            root = child
            child = root * 2 + 1  # 继续往后比较
        else:  # 如果父节点大于最大的孩子节点，直接退出循环，后面肯定全部小于父节点
            break


def dui_sort(nums: list):
    if len(nums) > 1:
        first = len(nums) // 2 - 1  # 得到最后一个父节点（索引）
        for start in range(first, -1, -1):  # 第一遍进行大堆的排序
            da_dui(nums, start, len(nums) - 1)
        for end in range(len(nums) - 1, 0, -1):
            nums[0], nums[end] = nums[end], nums[0]
            da_dui(nums, 0, end - 1)


data7 = copy.deepcopy(data)
dui_sort(data7)
print('7.堆排1：', data7)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

# 计数排序

import copy


# 8.计数排序：计数排序要求输入的数据必须是有确定范围的整数
# 它的优势在于在对一定范围内的整数排序时，它的复杂度为Ο(n+k)（其中k是整数的范围），快于任何比较排序算法。
# 当然这是一种牺牲空间换取时间的做法，而且当O(k)>O(n*log(n))的时候其效率反而不如基于比较的排序
# （基于比较的排序的时间复杂度在理论上的下限是O(n*log(n)), 如归并排序，堆排序）
def count_sort(nums: list):
    if len(nums) <= 1:
        return nums
    max_num = max(nums)  # 找出最大值的时候复杂度是多少呢？
    min_num = min(nums)  # 找出最小值的时候复杂度是多少呢？
    if min_num < 0:  # 实现负数的排序
        counts = [0] * (max_num - min_num + 1)
    else:
        counts = [0] * (max_num + 1)
    for i in nums:
        counts[i] += 1
    result = []
    if len(counts) > max_num + 1:  # 实现负数的排序
        for i in range(max_num + 1, len(counts)):
            for j in range(counts[i]):
                result.append(i - len(counts))
    for i in range(max_num + 1):
        for j in range(counts[i]):
            result.append(i)
    return result


data8 = copy.deepcopy(data)
print('8.计数1：', count_sort(data8))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

# 桶排序

# 9.桶排序,桶排序算法要求，数据的长度必须完全一样
def bucket_sort(nums: list):
    pass

1
2
3

# 基数排序

import copy


# 10.基数排序(桶子法)
def ji_shu_sort(nums: list):
    k = len(str(max(nums)))  # 最大值有几位
    radix = 10 * k
    bucket = [[] for _ in range(radix)]
    print(len(bucket))
    for i in range(1, k + 1):
        if i == 1:
            for val in nums:
                bucket[val % (radix * i)].append(val)  # 析取整数第K位数字 （从低到高）
        else:
            for val in nums:
                bucket[val // (radix * (i - 1))].append(val)
        print(bucket)
        del nums[:]
        for each in bucket:
            nums.extend(each)  # 桶合并
        bucket = [[] for _ in range(radix)]


data10 = [1, 3, 99, 23, 555, 89, 3, 1, 5, 89, 66]
ji_shu_sort(data10)
print('10.基数1：', data10)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

# 参考

1 (opens new window) 2 (opens new window) 3 (opens new window)

#Python

上次更新: 2024/02/24, 10:30:15

← zip压缩案例 django基础→